弾性応力波の伝播をFEMで解析する
このページは2006年6月16から開いています.

弾性応力波の伝播をFEMで解析する
このページは2006年6月16から開いています.

 英語版
英語版
|
All Rights Reserved by Dr. SHINOZUKA Jun.
|
物体が物体に衝突すると,衝突界面から応力波がそれぞれの 物体内部に伝播します. 応力も短い時間で見れば,物体内部を波として伝播します. 応力を波として考えるところが動的問題と静的問題の違いです. 衝突時に発生する応力の増分は,物体の密度と,応力波の伝播速度と, 物体内部の粒子速度の変化に比例します. 応力波には,弾性応力波と塑性応力波の二種類あります. 応力波の伝播速度は,弾性波の場合,物体の密度, ヤング率,ポアソン比で決まります(物体の音速). 一方,塑性波の場合は,物体の密度,と加工硬化係数 ,ポアソン比で決まります. どうちらも,材料の応力-ひずみ曲線の接線に依存します. 衝突界面で発生する応力は,応力増分を時間積分することで算出できます. 今,断面積が非常に小さい(棒の長さに比べて小さい)丸棒を考えると, 棒内を伝播する応力は,棒の軸方向に伝播する応力だけと見なせます.
ここで,衝突速度が比較的低速で,衝突界面で発生する応力が物体の 降伏応力を超えない場合を考えます. この場合,弾性波が両棒の中を伝播します. 衝突界面で発生した弾性波が通過した領域は,弾性変形します(粒子速度が変化している). 弾性波が,衝突界面と反対の端面に到達した時,応力波の反射がおこります. 端面が自由面である時,圧縮応力波が入射した場合,引張り応力波として反射されます. 入射波と反射波が重なった領域の応力は,重ね合わせの原理で0になります. 一方,端面が固定端である場合,圧縮応力波が入射した場合には,圧縮応力波 が反射し,両波が重なった領域では,応力の大きさは倍になります.
入力棒と出力棒の棒の長さが同じで,断面積も材料特性も同じである場合, 衝突してから,弾性波が入力棒の2倍の長さを伝播する時間後には, 入力棒は完全に停止し,出力棒は入力棒の衝突速度で移動します. この時,両棒の中には,応力波””重ね合わせ”で見かけ上,0になります. 見かけ上,応力が無いように見えますが,圧縮応力と引張り応力が延々と棒内部を 伝播しています. 出力棒の長さが,入力棒の長さよりも長い場合, やはり, 衝突してから弾性波が入力棒の2倍の長さを伝播する時間の後, 入力棒は完全に停止し,出力棒が動きだします. 入力棒は,重ね合わせの原理で見かけ上,応力は0ですが, 出力棒は,圧縮と引張り応力が残留し,交互に出力棒の中に出現します. つまり,出力棒は,弾性的に伸び縮みしながら,動いていきます. ちょうど,コイルバネが振動しなから,移動するようにです.
下図のアニメーションは,ある棒が静止している棒 に衝突した時,棒の中を伝播する 応力波を計算した例です. シミュレーションは, 陽解法による動的熱弾塑性FEMソフト(RDynFfem)で行いました.

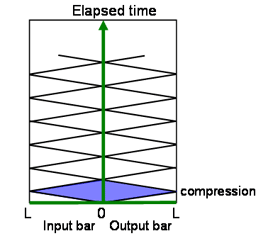
入力棒の長さと出力棒の長さの比が1:1の場合

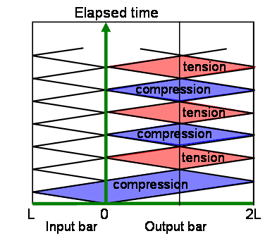
入力棒の長さと出力棒の長さの比が1:2の場合

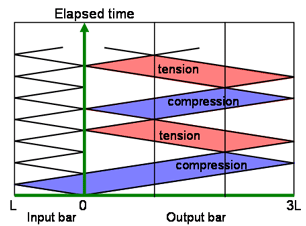
入力棒の長さと出力棒の長さの比が1:3の場合
解析した軸方向の応力分布です.

この図は,有効応力分布です.
ところで,出力棒の右端が固定端である場合,弾性応力波の伝播状態は,下図のようになります.

入力棒の長さと出力棒の長さの比が1:1の場合

入力棒の長さと出力棒の長さの比が1:3の場合
固定端の条件なので,圧縮応力波は固定端で圧縮応力として反射します. したがって重ね合わせの原理より,応力の大きさは2倍になります. 右端で濃い青色になる様子が分かると思います. 自由端の場合,入力棒は静止しますが, 固定端の場合,入力棒は逆向きの速度で移動しだします.
These results were simulated by the FEM software "RDynFem" that has been developed by Dr. SHINOZUKA Jun.